In my shift from the world of elementary school to middle school, I’ve noticed that we talk about mathematics instruction in different ways. Initially, I believed that we shared an understanding of how to engage students in number talks, use multiple representations, and structure classroom discourse to elicit student thinking and create a coherent thread of mathematical understanding. Working with my middle school team, I realized that while my colleagues had a deep understanding of the mathematics they taught, they were less familiar with the mathematical thinking students had done in earlier grades.
What foundational experiences occur in elementary school?
Our K–5 curriculum department and teachers had invested years in developing strategies for classroom discourse for mathematics and other content areas. Through books such as Elham Kazemi and Allison Hintz’s Intentional Talk and Sherry Parrish’s Number Talks, teachers in grades K–5 led robust classroom discussions centered on the ideas and strategies shared by students. When I moved to middle school, I realized that we often used the same words but these words had different meanings.
In many elementary classrooms, a Number Talk consisted of students sharing a variety of ways to find a solution. Before the correct answer was given, students shared the different methods they used. Often, there were three or four different ways students could approach a problem. For example, to solve 18 x 4, the teacher might record the following suggestions from students:
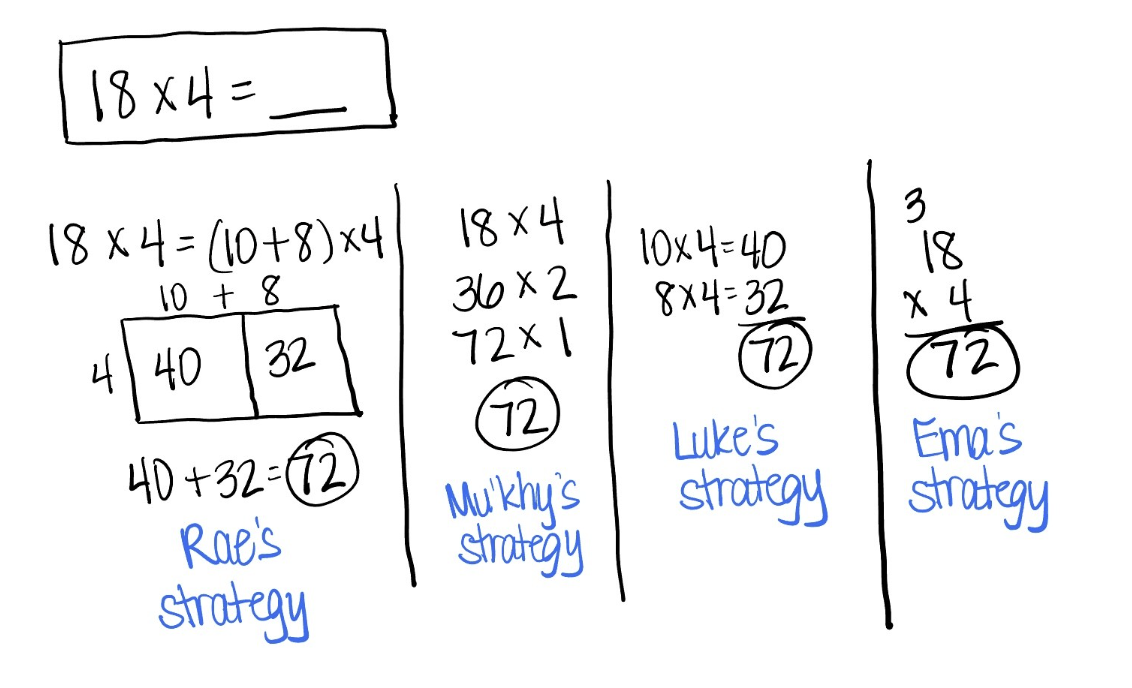
The conversation is often focused on connections between the strategies, relating to questions such as
- How does Rae’s strategy compare with Luke’s strategy? What is the same? What is different?
- Which of these strategies would you use to solve 27 x 5? Why would you use that strategy?
How do these elementary experiences translate to middle school?
When I mentioned using Number Talks to my middle school colleagues, they described having a student share an answer and provide reasoning for why it was correct. This might sound like what occurs in an elementary school classroom, but this description focused on sharing the correct answer and typically involved a single student’s response rather than sharing multiple strategies and discussing various approaches. Whereas our elementary classrooms were solving fewer problems and having in-depth conversations, it appeared that our middle school classrooms were focusing on repetition to build skills with calculation.
To be clear, I believe that students need opportunities to explore a variety of strategies and engage in conversations to make connections—while also having time to practice, apply, and refine skills. As I continued to grow in my role as a middle school teacher, I began to use the phrase “Elementary doesn’t necessarily do everything right, but they do things first.” Framing the conversation from this perspective invited teachers at the middle school level to be curious about what students were learning before they arrived in the middle school classrooms. I looked for times when I could connect what our middle school students were learning to what students had experienced in elementary school.
How might middle school teachers support students who are still working to master foundational skills?
Because multiplicative reasoning is foundational to building the proportional reasoning used in middle school mathematics, my conversations around content frequently involve methods for multiplication and division. Many middle school teachers “just know” their basic facts from memory, recalling that 4 x 8 is 32 or 7 x 9 is 63.

When students in elementary school are beginning to learn multiplication facts, they start with foundational facts, such as multiplying by 1, 2, and 5. As students develop fluency with the foundational facts, they use this knowledge to derive more complex multiplication facts. One way to derive 7 x 9 is to use the distributive property. As you can see in the photo, Daniel solved 7 x 9 as 7(5 + 4). Drawing an open array to organize his thinking, Daniel recalled that 7 x 5 is 35, then “broke apart” 4 as 2 + 2 to find the product of 7 x 4. To find the product of 7 x 9, Daniel added the parts from the open array for a final answer of 63.
For many teachers, particularly at middle school where fact fluency is essential, this method appears inefficient and laborious. In my current role, I work with students in grades 7 and 8 who are strengthening foundational concepts. As with any skill, the more students practiced, the more efficient they became with their multiplication facts. As a bonus, if they could not recall a multiplication fact, they were empowered to use the distributive property and move beyond counting strategies.
How can the strategies used for foundational skills extend to support current content standards (and beyond)?
Using the structure of the distributive property to develop fluency with multiplication facts provided a foundation to extend to multi-digit multiplication. Using the distributive property to solve 48 x 6, Claire multiplied 40 x 6 and 8 x 6 before adding the parts to find a final answer of 288.
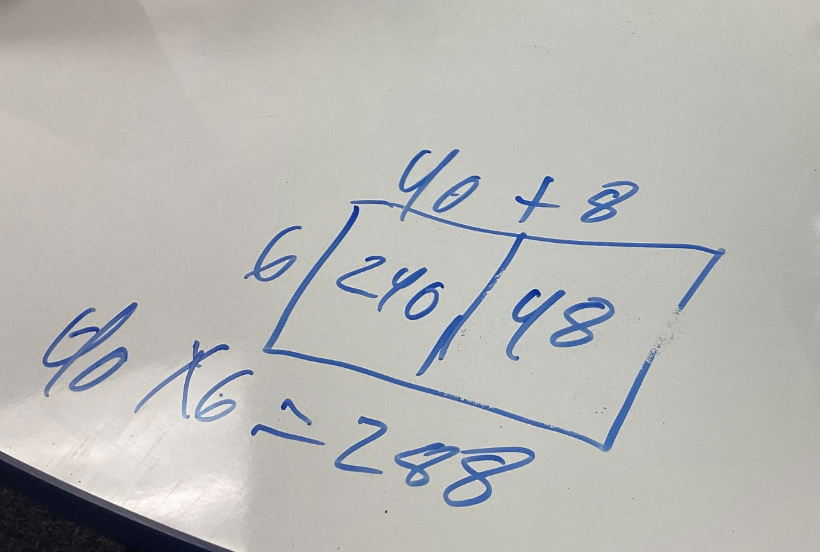
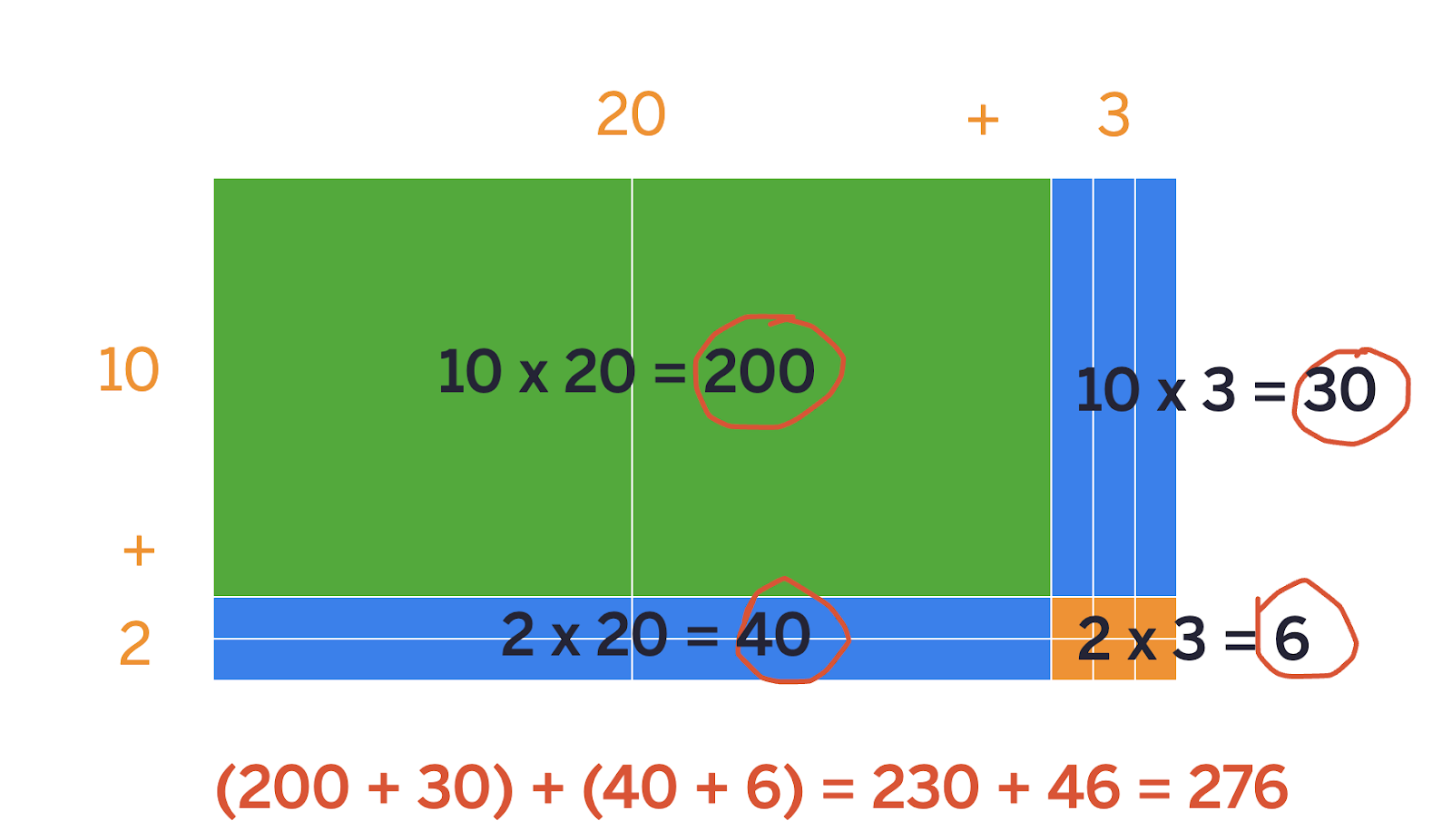
Modeling with the distributive property allows for greater flexibility in strategy choice, and the structure of an open array can be used to solve multiplication problems with any number of digits. This example shows how the distributive property might be used to solve 23 x 12.
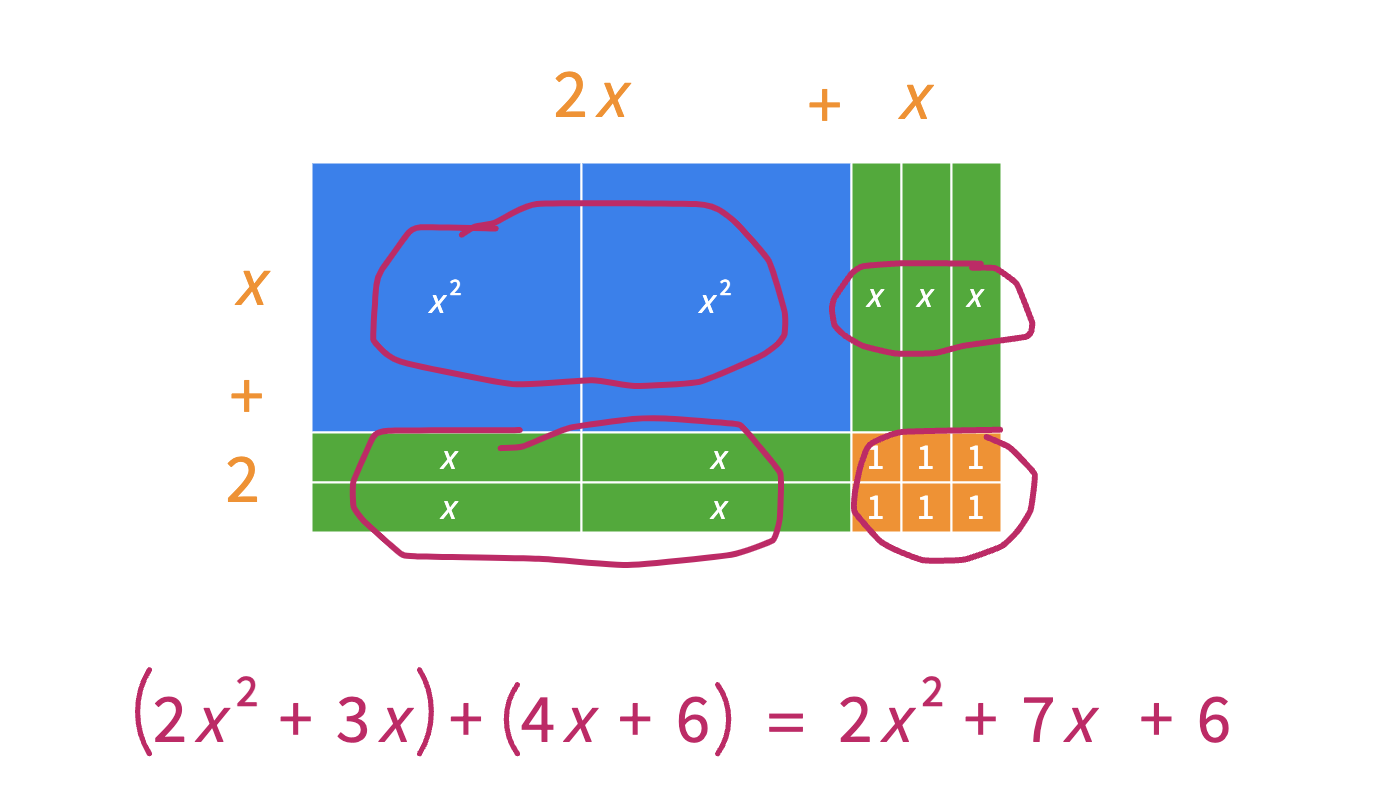
As students move from middle school to high school mathematics, the strategy that Rae described in the Number Talk to solve 18 x 4 extends to represent problems such as (2x + x)(x+2). Placing the representation for 23 x 12 alongside the representation for (2x + x)(x+2) can lead to powerful conversations where students begin to generalize the work they have been doing with multiplication since grade 3.
How can we work across grade levels to best support our students?
Regardless of the grade level or course that we teach, we want our students to develop a deep understanding and appreciation for the content. Rather than operating in the isolation of our grade-band groups, vertical and collaborative conversations can help teachers develop a more connected understanding of the curriculum to the benefit of our students. Learning from one another about where our students have been and understanding where they are going will lead to stronger coherence across grade levels—and a more enriching educational experience for our students.
Making an Impact
During a recent math department meeting, I shared this progression of reasoning about multiplication. Wondering how his students might use these ideas, one of our teachers introduced distributive property with students solving problems such as 49 x 8 and 256 x 7 with visual organizers. Several students shared that they found the work “easy” and “familiar,” so the teacher replied that they would be using letters in the following day’s lesson. One of the students responded, “Wait! I think I know what that is going to look like!” and proceeded to represent his thinking with this model:
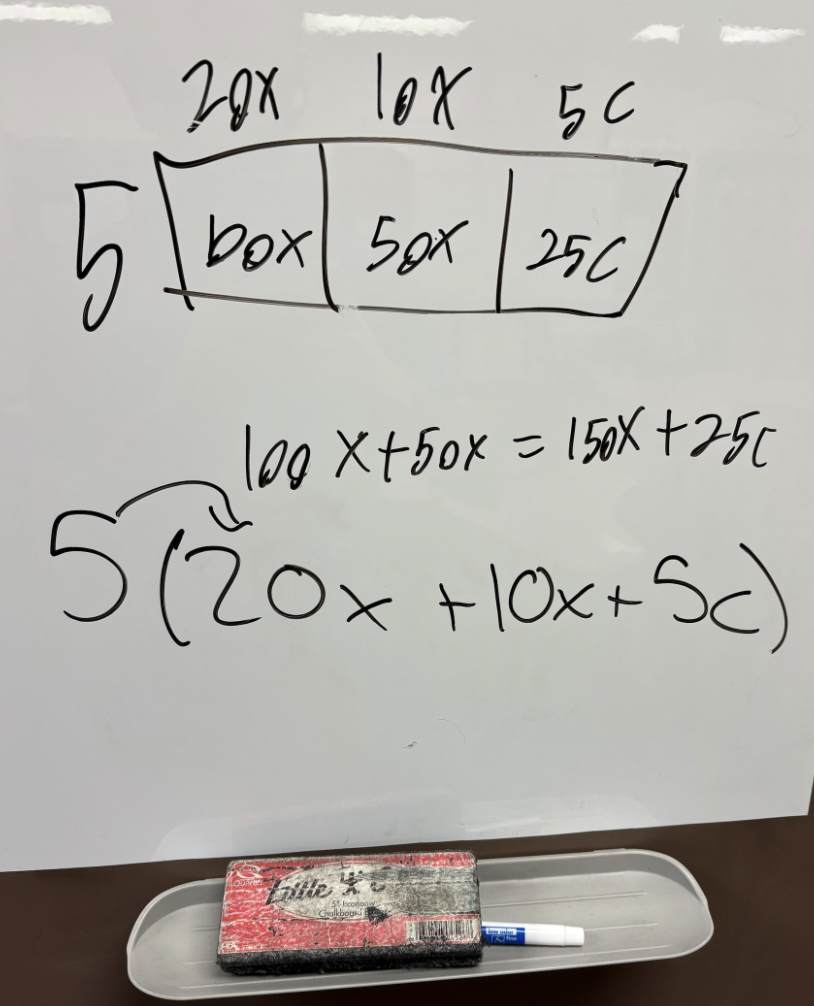
When the teacher relayed this experience to me, he said enthusiastically, “This has been the most exciting moment of my teaching career!” Encouraging students to build representations and models that make sense to them and allowing opportunities to experiment as they extend these models to new content makes for powerful learning that students will not easily forget! As teachers, one way we can help students develop these important connections is by strengthening our own understanding of skill progressions through vertical conversations.



