The language we use with students can clarify meaning—or cause confusion. Imagine a second-grade classroom where students are learning to subtract. In an attempt to help students, a teacher tells them that one always subtracts the smaller number from the larger number with an example such as 37 – 19. However, this can cause confusion when students are introduced to negative numbers. This “rule” can make math fuzzy for students even before they encounter negative numbers, such as students who say the difference of 37 – 19 is 22 because they solve 9 – 7, thinking that you always subtract from the larger number.
Providing opportunities for students to develop their own understanding of content is an essential part of building a deep understanding. Rather than relying on a narrow definition or algorithm for using mathematical tools and vocabulary, we want students to become accurate, efficient, and flexible in their understanding of how to use tools and procedures.
Developing Use of Number Lines
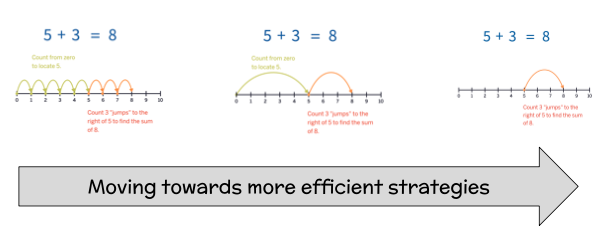
The use of tools and manipulatives are an important part of sense-making in mathematics. Although the use of a number line might appear fluid and effortless to an adult, there are several steps a student needs to consider—especially when first learning to use a number line. For example, students are often told to “begin at zero” to locate a number. For example, when solving 5 + 3, a student might
- begin at zero.
- move 5 “jumps” or spaces to the right to locate 5.
- count 3 additional “jumps” or spaces to the right.
- recognize that the location of 8 on the number line gives the sum of 5 + 3.
As they continue using number lines, mathematically proficient students often solve 5 + 3 by beginning at 5 and moving 3 spaces to the right rather than always beginning at zero. These students implicitly understand that the number line is a tool to help them model distances and that zero is a reference point.
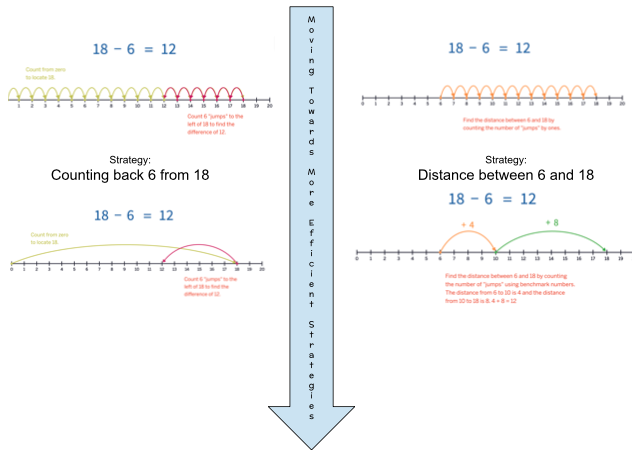
Shifting from Addition to Subtraction
Developing a flexible understanding of number line use can help students use a number line to solve 18 – 6. Rather than begin at zero, move to 18 and then count 6 to the left, efficient students focus on the distance between the numbers. They might begin at 6 and count the distance to 18, initially counting by ones before considering benchmarks or friendly numbers.
Leveraging Number Lines in Middle School
While working with two students recently to add and subtract integers, we found that the ways in which they used the number line differed. As they discussed their thinking, each student was convinced that they were correct. In solving -4 -8, they agreed on the solution of -12, but each thought their drawing was correct and the other drawing was incorrect.
To represent -4 -8 on a number line, Zoe drew this example:

Eli drew this example:

As they described their solution process, it became clear that each student thought about a different starting point for the expression. Zoe looked at -4, the first number in the expression, and plotted a point at that location. Eli started at 0 before jumping to -4.
This prompted an important classroom discussion about which model is “correct.” Eli explained that his teacher in elementary school told him that when using a number line, you always start at zero. Zoe said she knew the location of -4 so she used it as her starting point. The class agreed that the approaches were essentially the same. While they understood Eli’s thinking, some students preferred Zoe’s method because they found it more efficient. Others, like Eli, thought that the starting point had to be at zero.
Exploring Other Expressions
While the example for -4 – 8 is rather clear-cut in the starting point and direction of the operation, the number line becomes less easy to read when the arrows cross paths. For example, Zoe drew this example to represent -4 – (-6).

Because he always starts at zero, Eli represented -4 – (-6) this way:

At this point, many students found that beginning at zero made the use of the number line confusing. Rather than being a helpful strategy, it became a burden. Our conversation focused on using zero as a reference point, determining that negative numbers are to the left of zero, and positive numbers are to the right of zero. With a focus on distance, students determined that addition joined two distances (although a negative sign would reverse the direction of the distance).
With multiple opportunities to experiment, students developed their own “rules” for adding and subtracting integers. By the end of our exploration, Eli was no longer beginning at zero on the number line. For example, to solve -1 + x = 2, Eli marked a point at -1 and marked a point at 2, finding the distance between the two points to answer 3. He was solving equations with fluency, demonstrating accuracy, efficiency, and flexibility.

At the end of class, I asked him to show me how someone could solve -3 + x = 4 using a number line. Although he had not typically marked the distance between the numbers as counting by ones, he wanted to make his thinking very clear for the video. You will notice that to solve -3 + x = 4, Eli marks -3 and 4 on the number before counting the distance between them, finding a solution of 7.
Developing Flexible Thinkers
Although it might seem at times that our students are not listening, we need to remember that our words have power with them. When sharing tips to help students, we can be mindful about how to provide opportunities to develop flexible thinking. Through classroom discourse and modeling, we can focus conversations on how students are making meaning of representations. Rather than focus on a single procedure or tool, we can help students become flexible thinkers who can adapt strategies to support new ways of thinking.